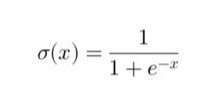Sigmoid 函數是一種常用的激活函數，主要用於神經網路中的非線性變換。它的數學表達式如下：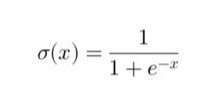

Sigmoid 函數的特性：

1. 輸出範圍：Sigmoid 函數的輸出範圍為 (0,1)(0, 1)(0,1)，這使得它非常適合處理需要將輸出解釋為概率的問題（如二分類問題）。
2. S 型曲線：Sigmoid 函數的圖像是一條平滑的 S 型曲線，這意味著它對於較大或較小的輸入值會趨近於 0 或 1，並且在接近 0 的區域，輸出變化最大。
3. 平滑和可微：Sigmoid 函數是平滑且可微的，這是神經網路中反向傳播算法所需要的特性。
   Sigmoid 函數的用途：
4. 二分類問題：Sigmoid 常用於二分類問題的輸出層，將神經網路的輸出轉換為介於 0 和 1 之間的概率值。比如，輸出值可以解釋為一個樣本屬於某一類的概率。
5. 邏輯回歸：在邏輯回歸中，Sigmoid 函數用於將線性回歸的輸出映射為概率。
   優點：

• 概率解釋：因為輸出值在 0 和 1 之間，Sigmoid 非常適合用於概率估計。
• 平滑過渡：它在中心區域的輸出變化平滑，能有效地學習輸入特徵之間的非線性關係。拜Sigmoid函數所賜，神經網路有大幅度的進步。